FIT file enhanced speed reading

Nick 3 days ago

Apologies if this seems like it's in the wrong category, but my question is not about FIT protocol, rather about which speed from a FIT file is representing what.

I see that in the FIT files, there is a record speed labelled enhanced, and also a GPS metadata speed labeled also as enhanced.

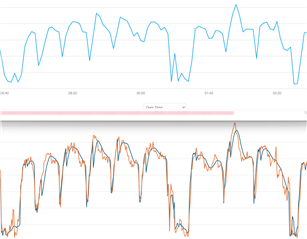
the issue is the GPS metadata appeares to be modified ( it's smoothed and generally lags in change ) compared with the Record speed.

Occasionally I see what I think looks like errors with the GPS metadata, particularly after a speed increase where it plataus or reduces

The Record speed looks as if it is more raw, but I can see a lot of variation in that, almost like it's using altimeter or accelerometer which creates noise for my purposes.

The Carming connect speed, is different yet again, but appears like a filtered record speed.

Anyone have anyidea at all which of these speeds are 2D instead of 3D, or which do not use the accelerometers?

GCM top, orange = record, blue = gps metadata

0 FlowState 2 days ago

I know you're not asking about the FIT protocol, but afaik "enhanced" speed (or "enhanced" anything) just means that the field has 32 bits of precision instead of the 16 bits associated with the unenhanced field. (And internally, the enhanced field incorporates the value of the unenhanced field.)

My educated guesses:

- the non-GPS speed record may use the accelerometer as a source, as well as GPS. (I don't know the details, but I do think Garmin uses the accel to help calculate current speed in some cases. The most obvious case is when GPS is temporarily unavailable, but people have also mentioned that Garmin may use some sort of hybrid algorithm which takes both GPS and accel into account)

- I wouldn't be surprised if GPS speed was smoothed/filtered

- As far 2D vs 3D speed goes, I assume that unless 3D speed is enabled in the activity settings (it's disabled by default), then all speed records would be 2D

If you really wanted to calculate "raw" instant GPS speed, would it be possible to use the difference in distance over small differences in time?

i.e.

speed = (d(n) - d(n-1)) / (t(n) - t(n-1))