I'm still not happy with CIQ Grade calcs. I live in Florida (mostly flat) so I really don't have a lot of real world opportunities to test Grade. On the other hand, these subtle rollers are some of the most challenging use cases to test the algorithm. The problem seems to be that barometric values aren't updated quickly - and then they tend to jump in a step function when they do change.
Even up steeper grades like Colorado passes that I got to ride last weekend, barometric data isn't smooth. A balance is needed between grade being noisey (due to barometric jumps) or slow to respond (due to smoothing out those jumps). I've tried to make the balance factor adaptive. So it detects a slope inversion or a transition to/from flat roads faster.
Even the native grade values are slow to respond. However, Garmin apparently did a lot of work on this problem in the new Garmin EDGE 1050 (according to DC Rainmaker's beta evals) and now the native grade is dramatically better. As soon as you hit a steep grade from a flat road, for example, grade will reflect a legit value, not slowly adjust over 10-15 seconds. Maybe using the accelerometer sensor to assist?
Anyway, Garmin still refuses to expose native Grade to CIQ. So we have to figure this out on our own.
I am thinking about a Community Effort to optimize the CIQ Grade calcs. I'll create a DF that only generates grade, and that writes to the FIT file, with some User Settings for various variables. I'll display the current grade as well as a line graph of grade to show how our algorithm adapts to slope changes, slope inversion, and transitions to/from flat roads. And I can display this and the EDGE's native grade on the same screen to compare.
I'll post the CIQ Code in GIT Hub and allow contributors to check out, and update. I bet we can come up with a barrel pretty quick that does a great job.
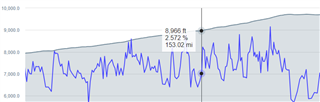
This image shows a pretty steep sustained grade (grey is the elevation profile, blue is my current GRADE calc). Now that I write a FIT graph I have more visibility into the dynamics and I clearly need to smooth it a bit more. I had tried a Kalman Filter at one point that also seemed ok, but not good enough.
If you are interested in joining the project, let me know.