What to the red-circled length measurements represent in the 66i (ver 9.20) screenshot below? One of the length measurements must be the calculated horizontal accuracy. Which one? And what is the other one?
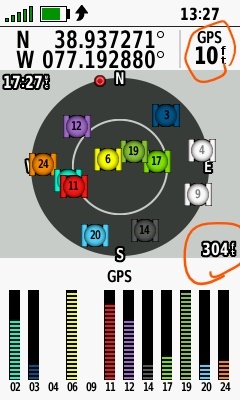
What to the red-circled length measurements represent in the 66i (ver 9.20) screenshot below? One of the length measurements must be the calculated horizontal accuracy. Which one? And what is the other one?

My only point here is that I remain curious what the 66i means when it says the reported location is within x feet of the displayed coordinates.
this means, if you give the calculated position to someone, let say by sms or so, and he also has portable GPS receiver, when he walks to this position within next minutes, he will find you there within a circle of about x feet diameter with high probability
this has noting to do with accuracy of the measurement or calculation
No, this is also not correct because the positional uncertainty compounds.
As Garmin stated, "...you would be within Xm of the true location."
If you record a point you could be Xm in any direction from it, and therefore the diameter of the area of uncertainty is 2X.
If you then provide the coordinates to someone else, and assuming all else is equal e.g. they have same equipment setup and conditions, assume 95%, then they also have the same positional uncertainty.
So if you are on the edge of your circle around the real coordinates, they could be on the edge of their circle for the reported position and on the opposite side. So the distance between you would be 2X, and the total of the combined area of uncertainty for them trying to relocate the point is a diameter of 4X because the uncertainty for them equally applies to the other side of your circle.
And it could be significantly more if either or both of your positions exceeds the 95%, and even worse again if the conditions are not ideal.
I agree, Wombo24, that 7m sounds like a long length here. But it's not so great if you consider I used it in the context of the two standard deviation uncertainty that was suggested by some unknown primary source.
I suspect you are correct that a 66i cannot differentiate a reflected signal from a direct signal. Assuming that's true, reflective distances would not be among the independent variables used in the function used by the device. That would be part of the answer to the question I posed: What does the 66i mean by "x ft"?.
As for how reflected signals affected my small sample, please keep in mind that all measurements were from the same position by the same device within the same 1.6 hours, during which no trees or surrounding two-story houses moved. I realize of course there could be some reflective error involved since the satellites are moving. So maybe some of my measurements that fell outside the stated uncertainty would have been within the uncertainty. For that reason, I may someday do a similar test where reflection is less likely. In the meantime, don't forget that I encourage people to run their own tests. I posted a link earlier to the Mathematica notebook. I believe it can be run from a browser without a Mathematica license. If anyone needs my help in that regard, please ask.
Also, I suspect, though I'm not certain, that your mention of a longer time is irrelevant, as is Skyeye's mention of "accuracy" verses precision. As I said earlier, my intuition is that increasing the time would increase the observed uncertainty without changing the calculated uncertainty. The device certainly has accurate estimates of time and expected satellite positions. I assume the relative positions of satellites to the device are independent variables to the function in question. Though again, that would be part of the answer to my question. For all I know, the function uses nothing more than the number of satellites above a certain signal strength. If you were to compare the measurements to a mythical "true" position, the average distance from that would be greater so that possibly fewer measurements would fall within the stated 10 ft.
A complete answer to my question might be too complicated for me to understand. But just knowing the independent variables used to calculate the "x ft" uncertainty and what quantity of uncertainty it is meant to show would be helpful along with whatever pertinent variables not taken into account.
As Garmin stated, "...you would be within Xm of the true location."
this lacks of one thing: what is true position and who told Garmin to define this? Someone has to define a point and call it reference. Then it is possible to collect calcuations referring to this particular value. There is no such thing as true position, so Garmin can not state that something is Xm of true position.
So if you are on the edge of your circle around the real coordinates, they could be on the edge of their circle for the reported position and on the opposite side. So the distance between you would be 2X, and the total of the combined area of uncertainty for them trying to relocate the point is a diameter of 4X because the uncertainty for them equally applies to the other side of your circle.
how can I be on the edge of a circle around real coordinates? What are real coordinates?
A receiver can be only somewhere and has some calculated position made of number of calculated positions over a period of time. This is the only reference. An estimated value, based on statistics over a number of measurements and calculations. Anythink like true position or real coordinates are not involved as they are not known.
Therefore if you send your displayed value to someone, he will arrive with high probability within the circle provided by the calculation of precision, provided other conditions do not change much in the mean time. Therefore it needs to be within short period of time, then the 95% can be fulfilled. Trying to do the same next day, the 95% probability will then no more be applicable.
Yes, clearly this applies to the other side as well, it has the problem, first, but when it arrives at the spot, conditions will be valid for both of them, thus kind of merge.
It has also be noted, that as all this concerns measured and calculated values only, let say in a city, you can see yourself on some maps then few hundred meters away from what you expect, e.g. two blocks away, but your GPS will still tell you precission figure of let say 10 meters.
As I mentioned in my previous post above, I agree with skyeye. About 15 years ago I did make the calculations that are described in the documented Wikipedia article above. I took readings at the exact same locations in my yard, three per day at least 3 hours apart for 10 days and a total of 30. I wanted them separated in time so that they would result in different satellites in different orbital locations. The main result was the Standard Deviation of the readings. As noted in the article, 1 SD includes 68% of all locations, 2 SDs includes 95% and 3 SDs includes 99.7%. Specifically, if the Standard Deviation is ±5 ft, then 95% of the values are between -10 ft and +10 ft from the average..
Your testing is great to see, developing a better understanding and appreciation of the device helps you to use it more effectively..or not so trusting and making your own more informed judgments as the case may be.
Your trees and buildings will be blocking satellites and introducing multipath, and those errors will be directional over time as the satellites move. Hence the longer observation times to balance the results. Blockage and multipath is the most significant issue with greatest impact.
There is a lot more in the estimation that goes on than just the geometry and SNR, the document linked earlier gives a list the the sorts of possible variables. Exactly what goes on I don't know and don't think you will find a list of what Garmin actually monitor in each device, or what conclusions are drawn from the variables. It's highly commercially sensitive information. And the GNSS firmware is often updated so it is likely changing also.
There is a reference and it’s called the WGS84 Reference Frame and it’s datum point in the earth is precisely known. That's how the whole system works.
The satellites are accurately tracked and their coordinates are calculated from ground stations with precisely known coordinates within the frame. One of the key methods used for tracking is laser.
The satellites are continually updated with their coordinates e.g. told where they are in relation to that point in the earth, and they continually re-transmit those positions along with the precise time the message is sent.
The receiver has it’s own clock and calculates the distances from the message transmission time from the satellites to work out it’s own coordinates in the frame based on all of those other “known”, “defined”, “true”, “real”, “reference” coordinates. It doesn’t have to “average” but may.
If you don’t accept that, then consider this.
The worlds major surface survey and mapping datum's are based on the GRS80 ellipsoid datum, and this is linked to the satellite WGS84 reference frame by only 0.1mm so effectively they are the same.
And an example in relation to the current US horizontal surface datum NAD83, from the US survey authority USGS: “… the increasing accuracy and availability of GPS has required two adjustments of the entire network. These adjustments produced new realizations that are still on the same datum: NAD83(NSRS2007), and NAD83(2011).”
You can read it here: https://geodesy.noaa.gov/datums/horizontal/north-american-datum-1983.shtml
So, if you were a US surveyor using an infrared Total Station to identify your location on the ground in relation to the surrounding ground survey marks (and you can’t get much more accurate than that) the principles are no different. And the datum's are the same.
And all measuring devices, including surveying instruments, have an accuracy specification of +/- something based on tests and distribution curves. No different to here.
The significant difference with satellites is that the baseline distances are much greater and so the unknown’s compound and are dynamic, things like the ionospheric effects and clock errors etc. And that’s why the accuracy for a consumer handheld is up around the meters level but the testing and statistical analysis that help the device to derive the accuracy estimate for ideal conditions is the same.
The reason you may see yourself hundreds of meters away in cities is because you are in far from ideal conditions. The buildings block visibility to many satellites and the receiver is subject to significant multipath (reflections) which travel further to arrive so skew the calculation result. The receiver can’t see them and can only assume they are correct.
You are still talking about accuracy when there is no such thing with portable gps receiver.
also in of the texts you copied is stated:
....Because the receiver cannot determine with respect to a known location in real time...
WGS84 is just a grid which was agreed on to have some common base to start with. There is not a point , but it is defined by x,y,z to space reference and major and minor diameter of the ellipsoid and data base of geoidal height.
So the receiver will attempt to make its calculation and then transform them into one of the ellipsoid or spheroid grids selected by the user. Here let says WGS84. It will apply the ellipsoid figures from the chart datum (this is not a point) and might apply some value of regional geoidal height to it.
Note that at this point the receiver has still no idea where it is and has no reference to WHS84 at all. How should it know where it is, who should tell the receiver where is his reference point is?
It would be different when using differential gps.
Let say JohnDear. Yes they make green tractors, but they are in fact one of the first companies who made differential gps for civilian market decades ago.
They mark for example a corner of a big field and decide this is our reference point. They are not that much curious where this is on WGS84 or other grid, but they define this is fixed point and calibrate their equipment to it.
Now they can apply life any differences a gps receiver calculates to the results. Now the tractors can have exact position and keep track on the field within few inches in real time. They basically remotely add or subtract some decimals from the calculated result of the gps receiver and use the new value for navigation.
In fact, meanwhile they provide such services not only for one field, but regional, but it is same workaround for mobile receivers.
This is possible, because we have now two values, even obtained by different way, and we do now compare them.
Here we can start speak about accuracy, as we compare a known value with measured value. And we need to know them at the same time to be able to recalculate our location data.
Such DGPS exist in many forms optimized for the user service in need, nautical , aeronautical, and other services needing local accuracy rather then just precision.
One attempt to optimize the calculation is WAAS/EGNOS, it tries to pass to the portable device some currently valid regional specific anomalies in reception of satellite signals, so the potential dilution of position value becomes smaller. But we know, it might do something, but it still is not able to replace correct functioning local DGSP system which refers to a predefined local reference point.
A few incorrect assumptions here.
Don’t get confused between the WGS84 reference frame and what you see as Garmin’s UTM projection based on WGS84 datum in the handheld. The name may be the same but they are very different things.
The WGS84 Reference Frame is an extremely accurate and precise 3D model all over the world and in space. You can’t see it but it’s at the heart of the GNSS system. It does have an origin point, like any datum it has to. And this one is critical because it is the exact centre of the earths mass which is what the satellites orbit around. Read here:
Extract: “The coordinate origin of WGS 84 is meant to be located at the Earth's center of mass; the uncertainty is believed to be less than 2 cm”
What you are seeing in the Garmin may be labelled “WGS84” but it’s not the 3D reference Frame, it’s a completely different beast. It’s one of the simplistic implementations I mentioned earlier that is based on the WGS84 datum but is a 2D projection. This is more a loose fit because of tectonic movement where the physical locations vs coordinates change over time. But it’s got nothing to do with how your device figures out its location, it’s only one method of how it can report out a 2D result to you.
And what you are referring to with the tractors is called RTK, and it does not work as a horizontal reference point.
The RTK rover continues to get its position from the satellites, that doesn’t change. It doesn’t get a horizontal reference from the base that is somehow used to project the rovers’ coordinates.
The base does know the exact coordinates of where it is, but only so it can calculate the errors in the satellite signal to its own position. It then sends those signal corrections to anybody anywhere on the link, not a horizontal reference. It has no idea where any rover is, it simply sends messages (RTCM) via a link to any rover that’s listening.
The rover then applies those same corrections to the signals it receives and so by removing some of the unknowns in the satellite signal it becomes more accurate.
However, because there is no horizontal reference it only works when both are in close proximity where the satellite signals are affected the same way at both ends. If the rover moves more than a few km from the base the accuracy drops and after 10 km or so can’t be used. Even when the base location may be known exactly.
As further proof, when I am doing RTK and if my rover moves under forest cover and loses satellites – even if it’s only a few meters away from my base it all falls apart because the rover positioning is from the satellites, not a horizontal reference. And that’s a key reason why RTK is common in agriculture because of all the typical open spaces and good satellite signal.
And finally, the word “accuracy” does not have to mean something is either extremely accurate…or not. It can have any number associated with it, it’s simply a measure of how accurate it is. Even if you may personally think it’s bad.
there is no need to talk abt how the WGS84 was created, it is one of the 'modern' systems which includes graviatation forces in as well, that abt why it is slightly different to other chart datum used worldwide for mapping purposes.
But it has a center, sure, as any other chart datum has also. The receiver just attempts to calculate the surface position from one grid to other, thought it has no reference on any of it. It does not care really, it can not find position on either grid, neither on some 'potsdam datum' nor WGS84 or what ever.
Any center of the chart datum is irrelevant here, as we can not measure the distance to it, nor can we place second receiver there to compare the results. We can only use reference freely accessible to us.
DGPS:
can not say exactly how different providers solve the task today, they are too many. At beginning, some tried to transmit same signal and acted as 'satellite', but doubt this is in use any more.
We had some system which used some frequencies in Ka band, but this was in the 90ties.
Today other communication means are used. This can be via sub-channel on common broadcasting FM stations, or on long wave broadcast as used for navigation of ships like becoming compulsory in Europe on the river Rhein.
The reference Points are somewhat more then 10km appart, AKAIK those of current JohnDear regions cover rather big areas, but still keep machines on track with 3 inches or so.
The matter is solely here that there is no reference for a portable receiver without such extra terrestrial installation. Also any other center of other grind models are of no interest , except as entry to the calculation formula.
The reference has to be on surface.
Is such reference agreed on, we can start talking abt accuracy of a device/system etc.
If we have no defined point we can agree on, we have no accuracy at all, as there is no such thing.
Accuracy does not mean something is right or not. It only tells us how far a measured value is from a known value. If I measure metal part previously measured and stated as 30mm with a caliper under same physical conditions, and my reading is 30.1mm, I have an expression on accuracy of my caliper or measuring method.
If I have some piece of metal of unknown dimension, measure it with my caliper, it tells me 30.1, with next try 30.15, with next try 30.05, then I can derive an expression about precision of my caliper or measuring method.
Both expressions are not interchangable
This is the whole point of the discussion.